Albert Einstein: “Die größte Erfindung des menschlichen Geistes? Die Zinseszinsen!”
Dieses Zitat vom bekannten Genie Albert Einstein bringt das heutige Thema auf den Punkt.
Heute beginne ich eine mehrteilige Serie über die Entwicklung wichtiger ökonomischer Kennzahlen seit dem es Aufzeichnungen darüber gibt. (Bzw. soweit diese Aufzeichnungen die im Internet auffindbar sind zurückreichen)
Die meisten Finanzseiten (und auch Bloomberg) bieten Daten maximal für etwa 50 Jahre. Daten die vor das 20. Jahrhundert zurückreichen sind sehr rar und ich konnte nur eine Seite im Netz finden, wo man diese herunterladen kann: http://www.measuringworth.com/. Diese Daten dürfen nur für “educational purpose” weiter benutzt werden, da der Financeblog mein privates Vergnügen ist und kein kommerzielles Interesse dahinter steht, sehe ich also keine Verletzung in den Urheberrechts-Bedigungen und werde deshalb die Daten von dieser Seite in aufbereiteter Form in meiner neuen Artikel-Serie verwenden.
Ich möchte in dieser Serie auch die historische Bewertung von Aktien beleuchten, sowie die historische Entwicklung von Wirtschaftsleistung, Inflation, etc. Wir werden in dieser Serie noch auf der Suche nach sich wiederholenden Mustern bei Wirtschaftszyklen, Zinsen, Aktienbewertung etc. sein.
Mir ist es aber am wichtigsten als erstes zu zeigen, welche atemberaubende Ergebnisse herauskommen, wenn man so eine lange Zeitspanne betrachtet. Der Effekt des Zinseszinses wird hier extrem deutlich.
Wie viel kann man in 100 Jahren verdienen, wenn man 100 USD investiert?
Eine sehr interessante, und faszinierende Frage, da dieser Anlagehorizont natürlich eine Generation bei weitem übersteigt. Die Resultate sind allerdings wirklich atemberaubend:
Zuerst ein kleines Beispiel:
Hätte man vor genau 100 Jahren, also im Jahr 1914 als der erste Weltkrieg ausgebrochen ist, 100 USD investiert, hätte man:
Am Geldmarkt (also am Konto bzw. am Sparbuch): Ende 2013 USD 2.354,99
In 10 jährigen Staatsanleihen bis Ende 2013: USD 25.493,88
In Aktien des S&P 500 inkl. Dividenden reinvestiert: USD 1.134.919,08
Das ist bereits eine beachtliche Entwicklung und auch ein beachtlicher Unterschied zwischen den einzelnen Anlageklassen.
Es ist schon faszinierend, wie aus USD 100,- innerhalb von 100 Jahren über 1 Million werden kann.
Noch extremer ist es, wenn man sich den Zeitraum seit 1830 ansieht – der Zeitraum in dem http://www.measuringworth.com/ Daten für alle relevanten Anlagemöglichkeiten liefern kann: Das sind 183 Jahre – also einige Generationen.
USD 100 für 183 Jahre angelegt – der Zinseszins in Aktion:
Am Sparbuch hätte man heute USD 32.237,66
In 10 jährige US-Staatsanleihen investiert hätte man heute USD 931.419,37
Und in Aktien des S&P 500 (total return, also Dividenden reinvestiert) hätte man heute sagenhafte USD 35.569.832,15
über 35 Millionen Dollar – für eine Investition von 100 Dollar vor 183 Jahren. Da es keine Zeitmaschine gibt könnten wir überlegen für unsere Ururur-Enkel einfach 100 EUR zu investieren 😉
Das faszinierende daran ist aber folgende Tatsache:
Die durchschnittliche Verzinsung der einzelnen Anlagemöglichkeiten seit 1830:
Wir haben also gesehen, daß es einen massiven Unterschied gemacht hat, ob man sein Geld auf das Sparbuch gelegt hat, in Anleihen oder in Aktien investiert hat.
Wie groß war nun bei den einzelnen Beispielen die jährliche Verzinsung?
Am Geldmarkt (Sparbuch, Konto) waren es 3,21% p.a.
Bei 10 jährigen Staatsanleihen waren es 5,12% p.a.
Bei Aktien des S&P 500 waren es 7,23% p.a.
Die Unterschiede wirken auf den ersten Blick nicht so gigantisch. Ob es nun 5% oder 7% pro Jahr sind scheint eigentlich nicht so relevant zu sein, doch wir haben gesehen, dass man in dem einen Fall aus den 100 USD ca. 1 Million machen konnte und im anderen Fall über 35 Millionen.
Das sind die Tücken des Zinseszinses und der Exponantialfunktion.
Der Zinseszins beruht genau auf so einer Exponentialfunktion:
Endkapital = Anfangskapital mal (1 + Zinssatz) hoch Anzahl Jahre
Bilder sagen mehr als 1000 Worte, deshalb habe ich einige Charts für den heutigen Beitrag vorbereitet:
Zuerst habe ich die Veranlagung am Geldmarkt, also kurzfristig und jederzeit verfügbar so wie am Sparbuch oder am Konto mit der Anlage in 10 jährige Staatsanleihen verglichen. Außerdem habe ich den Kurs des Dow Jones Index (dieser ist seit 1796 verfügbar) hinzugefügt. Es ist allerdings nur der Kurs, Dividenden werden hier ignoriert. Wir werden noch sehen, dass das einen gigantischen Unterschied macht.
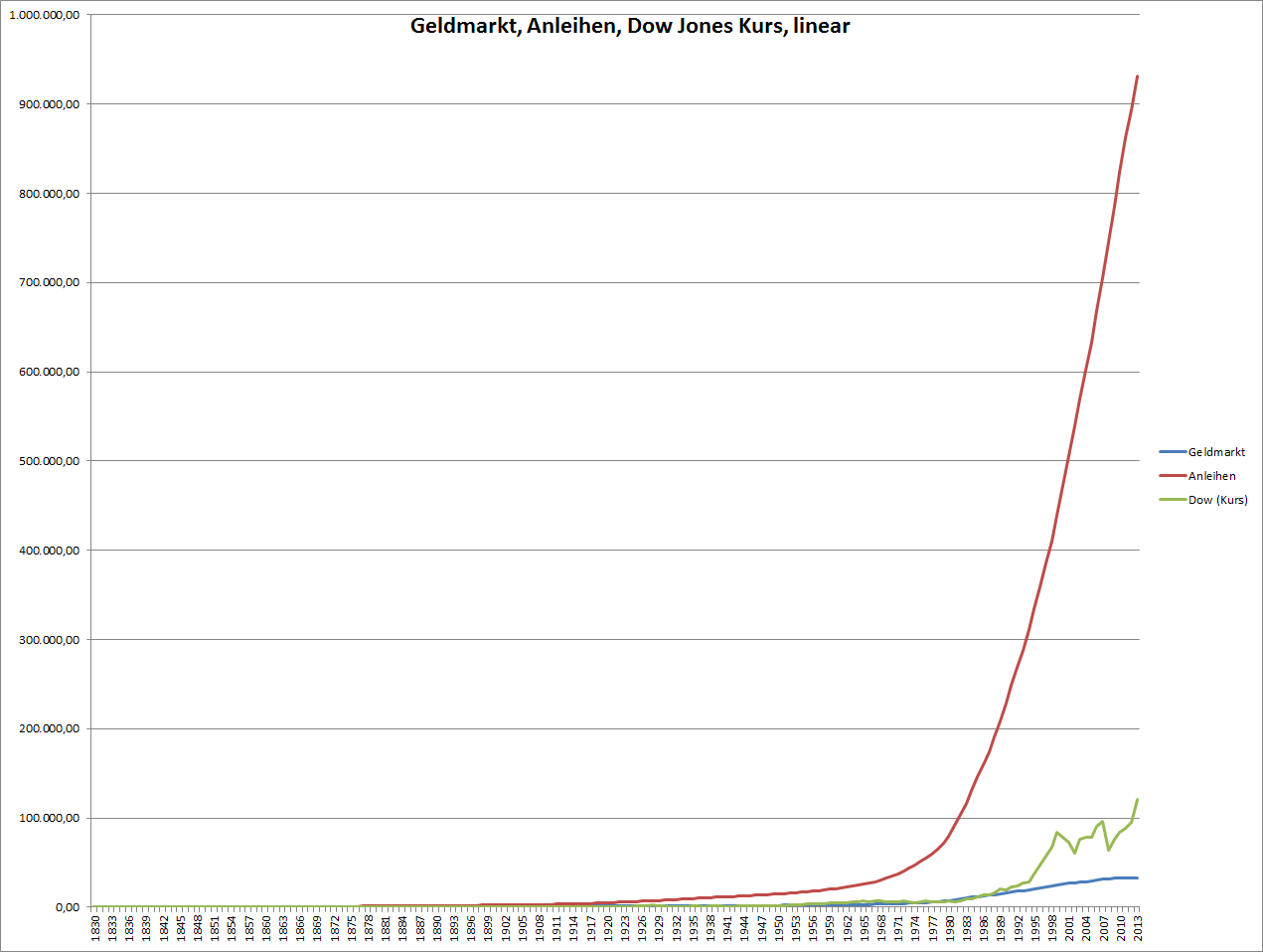
Hier ist der Charakter einer Exponantialfunktion sehr gut zu erkennen: Zuerst ein sanfter Anstieg, der immer steiler wirkt und schließlich in unermessliche Höhen steigt.
Der Unterschied zwischen einer Verzinsung von etwa 3% (Geldmarkt) und etwa 5%(Anleihen) ist eklatant. Dabei möchte man meinen, dass diese 2% Differenz nicht so viel ausmachen können. Je länger die Zeitreihe allerdings wird umso gigantischer wird diese Differenz.
Jetzt wird es noch extremer:
Bisher haben wir die Dividenden einfach ignoriert und in dem Vergleich nur den aktuellen Kurs des Dow Jones Index einbezogen. Die Veranlagung in 10 jährige Anleihen lässt den Dow Jones im ersten Chart richtig mickrig aussehen (grüne Linie).
Doch wir sieht es aus, wenn man auch die Dividenden berücksichtigt?
Aufzeichnungen über die Dividenden gibt es leider erst seit 1871, deshalb habe ich im nächsten Chart von 1830 bis 1871 den Kursindex genommen und ab 1871 dann die Dividenden berücksichtigt und natürlich auch reinvestiert (total return).
Der Vergleichschart: Geldmarkt, Anleihen und Aktien seit 1830:
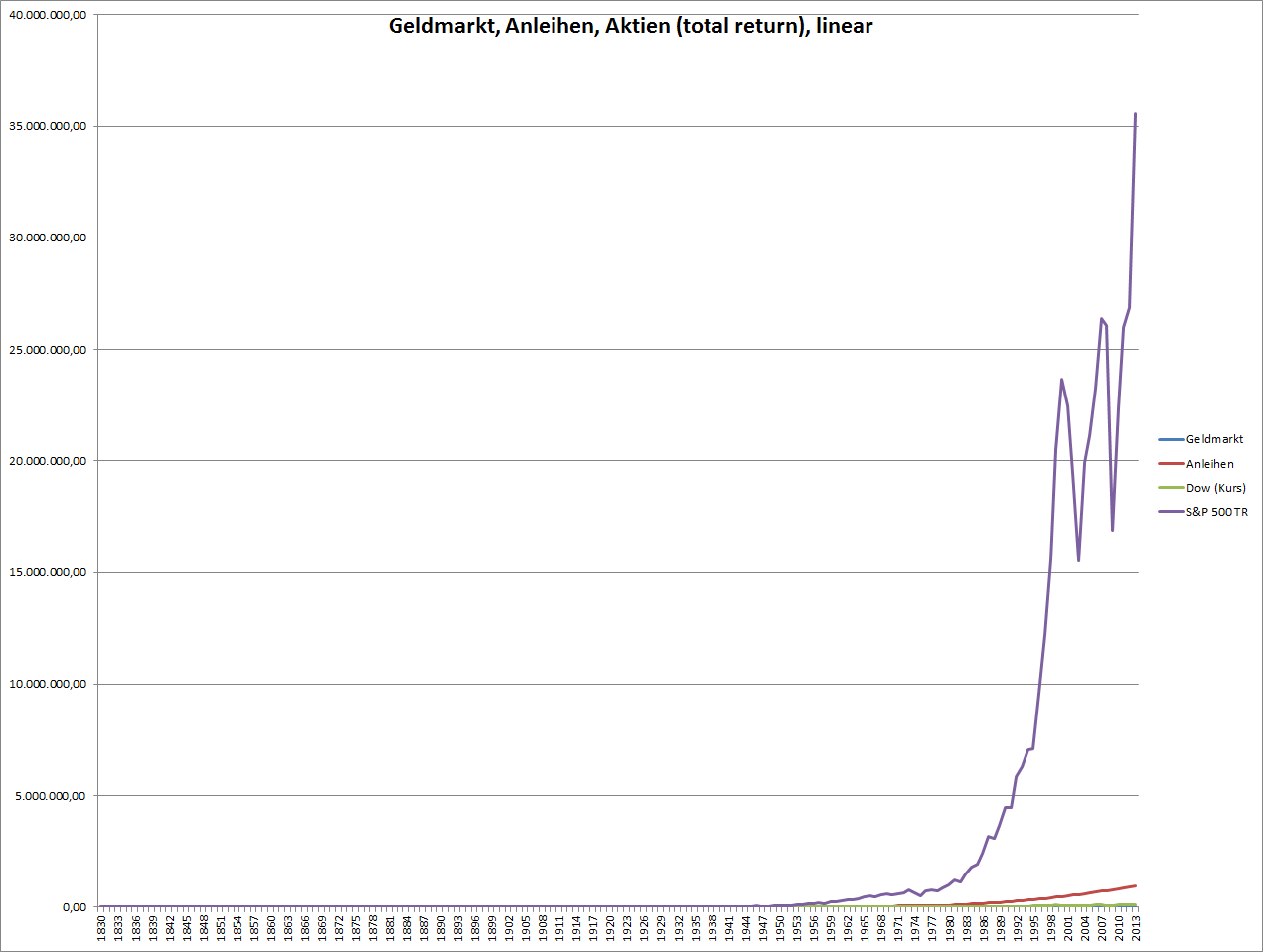
Der Zinseszins-Effekt schlägt erbarmungslos zu: Die rote Linie die vorher noch in den Himmel gewachsen ist, sieht jetzt im Vergleich zur violetten Linie für die Aktien inkl. Dividenden zwergenhaft aus.
Die Geldmarkt-Linie und die Kurslinie des Dow-Jones kann man gar nicht mehr erkennen.
Dabei ist der Unterschied er jährlichen Verzinsung der beiden Linien (rot für Anleihen und lila für Aktien) ebenfalls nur ca. 2% pro Jahr.
Daraus lernen wir:
1) Aktien-Kursindices sagen nicht viel über die vergangene Entwicklung aus, da sie Dividenden ignorieren: Beispiel: ATX, Dow Jones, S&P 500.
Hingegen ist z.B. der deutsche Aktienindex (DAX) ein sogenannter Performance-Index, welcher auch Dividendenzahlungen beachtet und reinvestiert. Ein längerfristiger Vergleich zwischen DAX und Dow Jones oder S&P 500 hinken also enorm.
Man sollte auch bei diversen Investment-Zertifikaten darauf achten, dass man auch die Dividenden bekommt- in vielen Fällen ist das nicht so, da sie auf Basis des Aktienkurses der betreffenden Aktien berechnet werden. Die Dividende steckt dann oft der Emmitent ein.
2) Der Zinseszins beruht auf der Exponentialfunktion, und diese ist für den menschlichen Hausverstand sehr schwer begreifbar.
3) Das predige ich sowieso immer: Aktien sind langfristig die beste Anlageform.
Der logarithmische Chart seit 1830:
Um die Entwicklung der Anlageklassen übersichtlicher zu machen, muss man nach einer Möglichkeit suchen diese Exponentialfunktion vom Zinseszins ein wenig “umzudrehen”. Dafür gibt es den Logarithmus: Die logarithmische Skala stellt auf der Y-Achse des Diagrammes jeweils 10 hoch x als eine Einheit dar, also 10 hoch 1 = 10, dann 10 hoch 2 = 100, 10 hoch 3 = 1000.
Logarithmisch betrachtet sieht der obige Chart dann so aus:
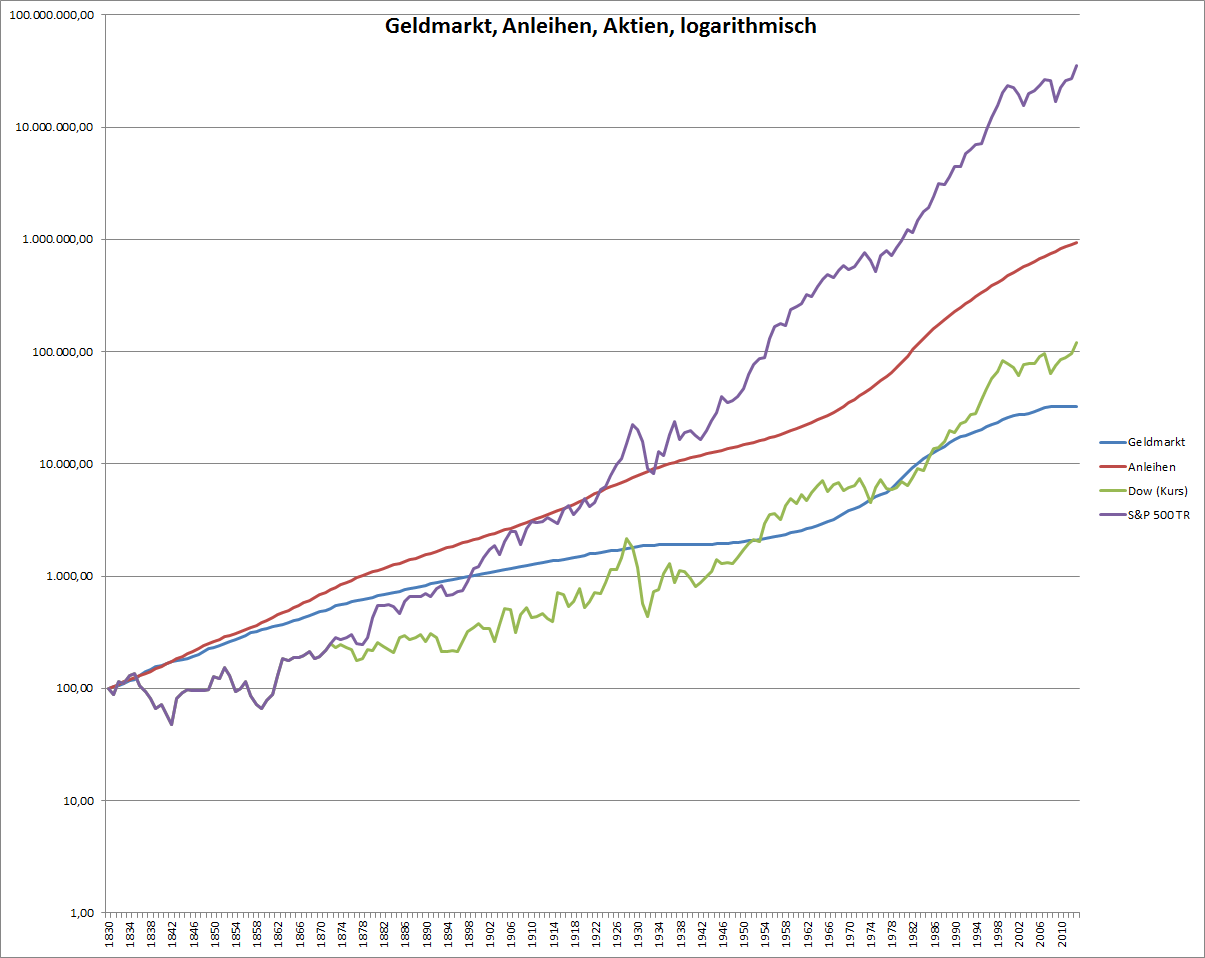
Man kann nun die Entwicklung der einzelnen Anlageklassen besser erkennen. Man sieht besser wann Einbrüche bei den Aktienkursen zu verzeichnen waren und wann die Zinsen für Spareinlagen oder Anleihen höher oder niedriger waren.
In den weiteren Artikeln werde ich das sowieso alles noch ausführlicher behandeln – auch den Zusammenhang zwischen Zinsen. Wirtschaftsleistung und Aktienkursen.
Aktien-Performance seit 1800 detailliert:
Nun habe ich noch eine Tabelle erstellt um im Detail zu zeigen, welchen Ertrag man mit Aktien in den letzten etwa 200 Jahren erwirtschaften konnte: In den Spalten ist das jeweilige Einstiegsjahr aufgetragen, also wann hat man begonnen zu investieren. In den einzelnen Zeilen sieht man dann den durchschnittlichen jährlichen Ertrag bei einer bestimmten Haltedauer (in Abstand von 5 Jahren).
Wenn man also z.B. 1880 Aktien des S&P 500 gekauft hat und für 10 Jahre gehalten hat, hatte man pro Jahr 5,11% Ertrag.
Die Daten von 1800 – 1870 sind leider ohne Berücksichtigung der Dividenden da ich nirgends die notwendigen Daten finden konnte.
| Kursperformance in % pro Jahr (Aktien, Dow Jones bis 1870, nachher S&P 500 Total Return) | |||||||||||
| Haltedauer | Kauf Jahr | ||||||||||
| Jahre | 1800 | 1820 | 1840 | 1860 | 1880 | 1900 | 1920 | 1940 | 1960 | 1980 | 2000 |
| 5 | 2,53% | 0,28% | 6,08% | 19,61% | 1,69% | 11,18% | 10,14% | 7,98% | 11,54% | 14,30% | -2,23% |
| 10 | -0,04% | 1,94% | 5,84% | 9,48% | 5,11% | 9,85% | 15,29% | 9,08% | 7,79% | 16,42% | -0,56% |
| 15 | 3,05% | 3,41% | 2,23% | 9,09% | 3,27% | 6,14% | 6,05% | 13,42% | 4,80% | 14,12% | 3,45% |
| 20 | 3,57% | -0,68% | 0,36% | 8,89% | 5,36% | 7,23% | 7,23% | 13,63% | 6,99% | 17,25% | |
| 25 | 2,90% | 0,64% | 3,94% | 7,41% | 6,50% | 7,80% | 7,38% | 13,21% | 8,42% | 13,07% | |
| 30 | 3,02% | 1,45% | 3,31% | 7,61% | 6,84% | 9,85% | 7,84% | 11,65% | 10,05% | 10,98% | |
| 35 | 3,50% | 0,56% | 4,01% | 6,44% | 5,69% | 6,72% | 9,84% | 9,76% | 9,99% | 11,13% | |
| 40 | 1,42% | -0,16% | 4,54% | 7,11% | 6,29% | 7,23% | 10,39% | 10,26% | 12,01% | ||
| 45 | 1,93% | 1,87% | 4,22% | 7,55% | 6,71% | 7,31% | 10,51% | 10,70% | 10,33% | ||
| 50 | 2,29% | 1,70% | 4,65% | 7,65% | 8,03% | 7,60% | 9,86% | 11,47% | 9,37% | ||
| 55 | 1,64% | 2,28% | 4,19% | 6,85% | 6,22% | 8,88% | 8,83% | 11,30% | 9,60% | ||
| 60 | 1,07% | 2,77% | 4,81% | 7,15% | 6,60% | 9,32% | 9,24% | 12,55% | |||
| 65 | 2,39% | 2,69% | 5,29% | 7,38% | 6,71% | 9,49% | 9,62% | 11,33% | |||
| 70 | 2,23% | 3,10% | 5,52% | 8,28% | 6,95% | 9,10% | 10,24% | 10,57% | |||
| 75 | 2,62% | 2,87% | 5,08% | 6,93% | 7,93% | 8,40% | 10,20% | 10,67% | |||
| 80 | 2,97% | 3,41% | 5,41% | 7,17% | 8,32% | 8,74% | 11,19% | ||||
| 85 | 2,89% | 3,85% | 5,68% | 7,22% | 8,51% | 9,06% | 10,35% | ||||
| 90 | 3,20% | 4,11% | 6,46% | 7,38% | 8,26% | 9,56% | 9,82% | ||||
| 95 | 3,02% | 3,84% | 5,51% | 8,13% | 7,75% | 9,57% | 9,93% | ||||
| 100 | 3,44% | 4,16% | 5,77% | 8,43% | 8,05% | 10,39% | |||||
| 105 | 3,80% | 4,44% | 5,88% | 8,58% | 8,34% | 9,75% | |||||
| 110 | 4,01% | 5,13% | 6,07% | 8,37% | 8,79% | 9,34% | |||||
| 115 | 3,79% | 4,41% | 6,74% | 7,95% | 8,83% | 9,46% | |||||
| 120 | 4,06% | 4,67% | 7,04% | 8,19% | 9,53% | ||||||
| 125 | 4,30% | 4,80% | 7,22% | 8,43% | 9,04% | ||||||
| 130 | 4,89% | 5,00% | 7,10% | 8,80% | 8,72% | ||||||
| 135 | 4,28% | 5,61% | 6,79% | 8,83% | 8,84% | ||||||
| 145 | 4,63% | 6,09% | 7,28% | 9,02% | |||||||
| 150 | 4,81% | 6,03% | 7,64% | 8,74% | |||||||
| 155 | 5,34% | 5,80% | 7,70% | 8,85% | |||||||
| 160 | 5,61% | 6,04% | 8,26% | ||||||||
| 165 | 5,78% | 6,28% | 7,93% | ||||||||
| 170 | 5,74% | 6,62% | 7,72% | ||||||||
| 175 | 5,54% | 6,71% | 7,84% | ||||||||
| 180 | 5,76% | 7,23% | |||||||||
| 185 | 5,98% | 6,96% | |||||||||
| 190 | 6,30% | 6,81% | |||||||||
| 195 | 6,38% | 6,94% | |||||||||
| 200 | 6,86% | ||||||||||